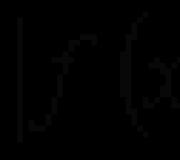Metodë për zëvendësimin e ndryshores kur integrimin e funksioneve. Integrimi duke zëvendësuar variablin (metoda e zëvendësimit)

Metoda bazohet në formulën e mëposhtme: ò f (x) dx \u003d ò f (j (t)) j` (t) dt, ku x \u003d j (t) është një funksion që është i diferencuar në intervalin në shqyrtim.

Dëshmi. Ne gjejmë derivatet në një ndryshore t nga pjesët e majtë dhe të djathtë të formulës.

Vini re se funksioni kompleks është i vendosur në pjesën e majtë, argumenti i ndërmjetëm i së cilës është X \u003d J (t). Prandaj, për ta dalluar atë nga t, së pari dallojnë integrimin e X, dhe pastaj derivativin e argumentit të ndërmjetëm nga T.

(Ò f (x) dx) `t \u003d (ò f (x) dx)` x * x` t \u003d f (x) j` (t)

Rrjedh nga ana e djathtë:

(Ò f (j (t)) j` (t) dt) `t \u003d f (j)) j '(t) \u003d f (x) j' (t)

Meqenëse këto derivativë janë të barabartë, me pasojat e teoremës së Lagranzhit, pjesët e majtë dhe të djathtë të formulës së provuar ndryshojnë në disa të përhershme. Meqenëse vetë integralet e pacaktuar janë përcaktuar me një saktësi të një komponenti të vazhdueshëm të pacaktuar, konstatuesi i treguar në regjistrin përfundimtar mund të hiqet. Provuar.

Variabli i zëvendësimit të suksesshëm ju lejon të thjeshtoni integralin origjinal, dhe në rastet më të thjeshta për ta zvogëluar atë në tryezë. Përdorimi i kësaj metode dallon metodat e një zëvendësimi linear dhe jolinear.

a) Metoda e zëvendësimit linear konsideron për shembull.

Shembulli 1. . Le t \u003d 1 - 2x, atëherë

dX \u003d D (½ - ½ t) \u003d - ½ dt

Duhet të theksohet se variabli i ri nuk mund të shkruhet në mënyrë eksplicite. Në raste të tilla, ata po flasin për transformimin e funksionit nën shenjën e diferencialit ose futjen e konstante dhe variablave nën shenjën e diferencialit, i.E. rreth zëvendësimi i nënkuptuar i ndryshores.

Shembulli 2. Për shembull, ne gjejmë òcos (3x + 2) dx. Sipas vetive diferenciale
dx \u003d (1/3) d (3x) \u003d (1/3) d (3x + 2), pastaj òcos (3x + 2) dx \u003d ò (1/3) cos (3x + 2) d (3x +
+ 2) \u003d (1/3) òcos (3x + 2) d (3x + 2) \u003d (1/3) mëkati (3x + 2) + C.

Në të dyja shembujt e konsideruar, një zëvendësim linear t \u003d kx + b (k ¹ 0) është përdorur për të gjetur integrals.

Në përgjithësi, teorema e mëposhtme është e vlefshme.

Teorema e zëvendësimit linear. Le të jetë f (x) të jetë një primitiv për funksionin f (x). Pastaj òf (kx + b) dx \u003d (1 / k) f (kx + b) + c, ku k dhe b janë disa konstante, k ¹ 0.

Dëshmi.

Sipas përkufizimit të integralit òf (kx + b) d (kx + b) \u003d f (kx + b) + c. ho
D (kx + b) \u003d (kx + b) `dx \u003d kdx. Unë do të sjell një shumëfishues të përhershëm K për shenjë të integralit: kòf (kx + b) dx \u003d f (kx + b) + C. Tani mund të ndani pjesët e majtë dhe të djathtë të barazisë në K dhe të merrni pohimin e provuar me një saktësia në përcaktimin e kushteve të përhershme.

Ky teoremë argumenton se nëse në përkufizimin e integralit ò f (x) dx \u003d f (x) + c në vend të argumentit x për të zëvendësuar shprehjen (kx + b), atëherë kjo do të çojë në paraqitjen e një faktor shtesë e 1 / k para primitive.

Përdorimi i teoremës së provuar do të zgjidhë shembujt e mëposhtëm.

Shembulli 3.

Ne do të gjejmë. Këtu kx + b \u003d 3 - x, i.e. k \u003d -1, b \u003d 3. Pastaj

Shembulli 4.

Ne do të gjejmë. Këtu kx + b \u003d 4x + 3, i.e. k \u003d 4, b \u003d 3. Pastaj

Shembull 5.

Ne do të gjejmë. Këtu kx + b \u003d -2x + 7, i.e. k \u003d -2, b \u003d 7. Pastaj

.

Shembulli 6.Ne do të gjejmë. Këtu kx + b \u003d 2x + 0, i.e. k \u003d 2, b \u003d 0.

.

Krahasoni rezultatin e marrë me shembullin 8, i cili është zgjidhur nga metoda e dekompozimit. Zgjidhja e së njëjtës detyrë në një metodë tjetër, kemi marrë përgjigjen . Krahasoni rezultatet e fituara :. Kështu, këto shprehje ndryshojnë nga njëri-tjetri për një term të përhershëm, i.E. Përgjigjet e marra nuk bien në kundërshtim me njëri-tjetrin.

Shembulli 7.Gjej . Ne theksojmë sheshin e plotë në emërues.

Në disa raste, zëvendësimi i ndryshores nuk e zvogëlon integruesin direkt në tavolinë, por mund të thjeshtojë zgjidhjen duke bërë të mundur përdorimin në hapin pasues të metodës së dekompozimit.

Shembulli 8.Për shembull, ne do të gjejmë. Replace t \u003d x + 2, pastaj dt \u003d d (x + 2) \u003d DX. Pastaj

ku C \u003d C 1 - 6 (kur zëvendëson në vend të shprehjes (x + 2), në vend të dy komponentëve të parë, ne marrim ½x 2 -2x - 6).

Shembulli 9.Ne do të gjejmë. Le t \u003d 2x + 1, pastaj dt \u003d 2dx; Dx \u003d ½ dt; X \u003d (t - 1) / 2.

Zëvendësim në vend të shprehjes (2x + 1), kllapa të hapura dhe jepni të ngjashme.

Vini re se në procesin e transformimeve, ne kaluam në një term tjetër të vazhdueshëm, sepse Grupi i kushteve të përhershme në procesin e transformimeve mund të hiqet.

b) Metoda e zëvendësimit jolinear konsideron për shembull.

Shembulli 1. . Le t \u003d - x 2. Tjetra, do të ishte e mundur të shprehim x deri në t, pastaj të gjesh një shprehje për DX dhe të zbatojë zëvendësimin e ndryshores në integrale. Por në këtë rast është më e lehtë të bësh ndryshe. Ne gjejmë dt \u003d d (-x 2) \u003d -2xdx. Vini re se shprehja XDX është një fabrikë e shprehjes integrand të integrimit të dëshiruar. Express atë nga barazia e fituar xdx \u003d - ½ dt. Pastaj

\u003d Ò (- ½) e t dt \u003d (- ½) ò e t dt \u003d (- ½) e t + c \u003d (- ½) + c

Merrni parasysh disa shembuj të tjerë.

Shembulli 2.Ne do të gjejmë. Le t \u003d 1 - x 2. Pastaj

Shembulli 3.Ne do të gjejmë. Le t \u003d. Pastaj

Shembulli 4.Në rastin e një zëvendësimi jolinear, është gjithashtu i përshtatshëm për të përdorur zëvendësimin e nënkuptuar të ndryshores.

Për shembull, ne do të gjejmë. Ne shkruajmë XDX \u003d.
\u003d (-1/4) d (3 - 2x 2) (zëvendësoi në mënyrë implicite variable t \u003d 3 - 2x 2). Pastaj

Shembull 5.Gjej . Këtu, gjithashtu, ne do të prezantojmë një ndryshore për shenjën e diferencialit: (zëvendësimi i nënkuptuar t \u003d 3 + 5x 3). Pastaj

Shembulli 6.Ne do të gjejmë. Për aq sa,

Shembulli 7.Ne do të gjejmë. Që, kjo

Konsideroni disa shembuj në të cilët ka nevojë për të kombinuar zëvendësime të ndryshme.

Shembulli 8.Gjej . Lë
t \u003d 2x + 1, pastaj x \u003d (t - 1) / 2; DX \u003d ½ dt.

Shembulli 9.Gjej . Lë
t \u003d x - 2, atëherë x \u003d t + 2; Dx \u003d dt.

Kur llogaritni integrale të caktuara duke përdorur formulën Labnic Newton, është e preferueshme që të mos dalloni hapat e zgjidhjes së problemit (gjetja e një funksioni të integruar primitiv, degjenerimi i rritjes primare). Një qasje e tillë duke përdorur, në veçanti, formulën për zëvendësimin e ndryshores dhe integrimin në pjesë për një integral të veçantë, zakonisht ju lejon të thjeshtoni zgjidhjen e zgjidhjes.

Teorema. Supozoni se funksioni φ (t) ka një derivat të vazhdueshëm në segmentin [α, β], a \u003d φ (α), b \u003d φ (β) dhe funksioni f (x) është i vazhdueshëm në secilën pikë x të llojit x \u003d φ (t), ku t [α, β].

Pastaj barazia e mëposhtme është e vërtetë:

Kjo formulë quhet një formulë zëvendësuese e ndryshueshme në një integral të veçantë.

Ashtu siç ishte në rastin e një integrimi të padefinuar, përdorimi i një zëvendësimi të ndryshueshëm ju lejon të thjeshtoni integralin, duke e çuar në tryezë (tabelore). Në të njëjtën kohë, në kontrast me një integral të pacaktuar në këtë rast, nuk ka nevojë të kthehet në ndryshoren fillestare të integrimit. Është e mjaftueshme vetëm për të gjetur kufijtë e integrimit të α dhe β përgjatë variablit të ri t si një zgjidhje në krahasim me ekuacionet e ndryshueshme φ (t) \u003d A dhe φ (t) \u003d in. Në praktikë, kryerja e një ndryshimi në variabël, shpesh fillon me faktin se shprehja t \u003d ψ (x) tregohet nga ndryshuesi i ri përmes një të vjetër. Në këtë rast, vendndodhja e integrimit të ndryshores T është thjeshtuar: α \u003d ψ (a), β \u003d ψ (b).

Shembull 19. Llogaritni

Vënë t \u003d 2-x 2. Pastaj dt \u003d d (2-x 2) \u003d (2-x 2) "dx \u003d -2xdx dhe xdx \u003d -dt. Nëse x \u003d 0, atëherë t \u003d 2-0 2 \u003d 2, dhe nëse x \u003d 1, atëherë T \u003d 2-1 2 \u003d 1. Rrjedhimisht:

Shembulli 20. Llogaritni

Ne përdorim zëvendësimin e ndryshueshëm. Pastaj dhe. Nëse x \u003d 0, atëherë t \u003d 1 dhe, nëse x \u003d 5, atëherë t \u003d 4. Kryerja e një zëvendësimi, marrim.

Ne kthehemi në shqyrtimin e rastit të përgjithshëm - metodën e zëvendësimit të variablave në një integrim të pacaktuar.

Shembull 5.

Si shembull, merrni pjesë integrale që ne kemi konsideruar në fillim të mësimit. Siç kemi folur tashmë, për të zgjidhur integrale, një formulë tabelare ,

dhe do të ishte gjithçka që unë do të doja ta redukoja.

Ideja e metodës së zëvendësimit është të shprehje komplekse (ose disa funksione) zëvendësohet me një letër.

Në këtë rast, sugjeron:

Letra e dytë më e popullarizuar për zëvendësim është letra z.. Në parim, letra të tjera mund të përdoren, por ne ende do t'i përmbahemi traditave.

Por kur zëvendësojmë ne kemi dx! Ndoshta, shumë menduan se nëse kalimi në një ndryshore të re t., në një pjesë integrale të re, gjithçka duhet të shprehet përmes letrës t., dhe diferenciale dxnuk ka fare vend. Ndjek një përfundim logjik që dx nevojë për të të kthehet në një shprehje të caktuar që varet vetëm ngat..

Veprimi tjetër. Pasi kemi marrë një zëvendësim, ky shembull është, ne duhet të gjejmë diferencën dt..

Tani sipas rregullave të proporcionit, ne shprehim dx:

.

Në këtë mënyrë:

.

Dhe kjo është tashmë më e madhe se as nuk ka një integral tabelare

(Tabela, integrals, natyrisht, është e vlefshme për të dy ndryshoren t.).

Në përfundim, mbetet të zëvendësohet. Mos harroni se.

Dizajni i fundosur i shembullit të konsideruar duhet të duket diçka e tillë:

Ne do të zëvendësojmë:, atëherë

.

.

Ikona nuk mban ndonjë kuptim matematik, ai nënkupton që ne ndërpresim zgjidhjen për shpjegime të ndërmjetme.

Kur aplikoni për një shembull në një fletore, shënimi i kundërt është bërë më mirë me një laps të thjeshtë.

Vëmendje! Në shembujt e mëposhtëm, gjetja e diferencës së ndryshores së re nuk do të përshkruhet në detaje.

Mos harroni mënyrën e parë për të zgjidhur:

Qfare eshte dallimi? Nuk ka dallim themelor. Kjo është në të vërtetë e njëjta gjë.

Por, nga pikëpamja e dizajnit të punës, metoda e rreshtimit të funksionit nën shenjën e diferencës është shumë më e shkurtër.

Lind pyetja. Nëse mënyra e parë është më e shkurtër, atëherë pse përdorni metodën e zëvendësimit? Fakti është se për një numër integralësh nuk është aq e lehtë për të "përshtatur" funksionin nën shenjën e diferencialit.

Shembulli 6.

Gjeni një integral të pacaktuar.

.

Ne do të zëvendësojmë:

;

.

Siç mund ta shihni, si rezultat i zëvendësimit, integrali fillestar është thjesht i thjeshtuar - është bërë një funksion i zakonshëm i energjisë. Ky është qëllimi i zëvendësimit - për të thjeshtuar integralin.

Njerëzit e avancuar dembel do ta zgjidhin lehtësisht këtë metodë integrale për të përmbledhur shenjën diferenciale:

Një tjetër gjë është se një vendim i tillë është i dukshëm jo shumë për të gjithë studentët. Përveç kësaj, në këtë shembull, përdorimi i një metode për të përmbledhur një funksion nën shenjën e diferencialit në mënyrë të konsiderueshme rrit rrezikun për t'u hutuar në zgjidhjen.

Shembulli 7.

Gjeni një integral të pacaktuar

Kryeni kontroll.

Shembulli 8.

Gjeni një integral të pacaktuar.

.

Vendimi: Ne prodhojmë një zëvendësim :.

.

Mbetet për të gjetur se çfarë do të kthehet xdx? Herë pas here, mashtrimi i mëposhtëm gjendet gjatë zgjidhjes integrale: x.ne shprehim mua nga i njëjti zëvendësim:

.

Shembulli 9.

Gjeni një integral të pacaktuar.

Ky është një shembull për një zgjidhje të pavarur. Përgjigja në fund të mësimit.

Shembulli 10.

Gjeni një integral të pacaktuar.

Somny, disa vënë re se tabela e referencës nuk ka një rregull zëvendësimi të ndryshueshëm. E bëri atë me vetëdije. Rregulli do të kontribuonte në konfuzionin në shpjegimin dhe mirëkuptimin, pasi në shembujt e mësipërm nuk duket në mënyrë eksplicite.

Është koha për të treguar rreth sfondit kryesor të përdorimit të një metode zëvendësuese të ndryshueshme: në shprehjen integruese duhet të ketë disa funksione dhe derivativin e saj . Për shembull, si : .

F.unnque, mund të mos jetë në punë, por në një kombinim tjetër.

Në këtë drejtim, kur të gjeni integrals, shpesh është e nevojshme të shikoni në tabelën e derivateve.

Në këtë shembull, 10 vërejnë se shkalla e numeratorit për njësi më pak emërues. Në tabelën e derivateve gjejmë një formulë që vetëm ul një diplomë për njësi. Dhe, kjo do të thotë, nëse përcaktoni t.emërues, atëherë shanset janë që numëruesi xdx do të kthehet në diçka të mirë:

Zëvendësimi: .

Nga rruga, nuk është aq e vështirë për të përmbledhur funksionin nën shenjën e diferencës:

Duhet të theksohet se për fraksionet, duket, një fokus i tillë nuk do të kalojë (më saktësisht, do t'ju duhet të aplikoni jo vetëm pritjen e zëvendësimit).

Integrimi i disa fraksioneve mund të mësohen në klasë Integrimi i fraksioneve komplekse. Këtu është një palë shembujsh tipikë për një zgjidhje të pavarur për të njëjtën metodë.

Shembulli 11.

Gjeni një integral të pacaktuar

Shembulli 12.

Gjeni një integral të pacaktuar

Zgjidhje në fund të mësimit.

Shembulli 13.

Gjeni një integral të pacaktuar

.

Ne shikojmë në tryezën e derivateve dhe gjejmë arccosine tonë: Meqë kemi Arquosinus dhe diçka të ngjashme me derivativin e saj në integrand.

Rregulla e përgjithshme:

Mbrapa t.ne tregojmë vetë funksionin(dhe jo derivativin e saj).

Në këtë rast: . Mbetet për të gjetur se çfarë do të kthehet pjesa tjetër e shprehjes fillestare

Në këtë shembull, gjetja d. t. shkoni në detaje sepse funksioni kompleks:

Ose, me pak fjalë:

.

Sipas sundimit të proporcionit, ne shprehim pjesën tjetër që na nevojitet: .

Në këtë mënyrë:

Shembulli 14.

Gjeni një integral të pacaktuar.

.

Një shembull për një zgjidhje të pavarur. Përgjigja është shumë afër.

Lexuesit e vëmendshëm vënë re se ne pamë disa shembuj me funksione trigonometrike. Dhe nuk është rastësisht, pasi nën dhe ntegerls nga funksionet trigonometrike Mësimet e ndara janë ndarë 7.1.5, 7.1.6, 7.1.7. Për më tepër, ka disa udhëzime të dobishme për të zëvendësuar variablin, i cili është veçanërisht i rëndësishëm për teapot, jo gjithmonë dhe jo menjëherë të qartë se çfarë lloj zëvendësimi duhet të kryhet në një integral të veçantë. Gjithashtu, disa lloje të zëvendësimeve mund të shihen në nenin 7.2.

Më shumë studentë me përvojë mund të njohin veten me zëvendësim tipik në integrals me funksione irracionale

Shembulli 12: Zgjidhja:

Ne do të zëvendësojmë:

Shembulli 14: Zgjidhja:

Ne do të zëvendësojmë:

Duke zëvendësuar një ndryshore në një integral të pacaktuar. Formulën e transformimit të diferencialeve. Shembuj të integrimit. Shembuj të zëvendësimeve lineare.

Shiko gjithashtu: Tabela e integrals të pacaktuar
Funksionet kryesore elementare dhe pronat e tyre

Metoda e zëvendësimit të ndryshores

Duke zëvendësuar variablin, ju mund të llogarisni integrals të thjeshtë dhe, në disa raste, thjeshtoni llogaritjen e më kompleksit.

Metoda e zëvendësimit të variablës është se ne jemi nga ndryshuesi i integrimit origjinal, le të jetë X, të shkojmë në një tjetër ndryshore, e cila është shënuar si t. Në të njëjtën kohë, ne besojmë se variablat x dhe t janë të lidhur me disa raporti x \u003d x (t), ose t \u003d t (x). Për shembull, x \u003d ln t., x \u003d sin T., T \u003d. 2 x + 1, etj. Detyra jonë është të zgjedhim një varësi të tillë midis X dhe T në mënyrë që integrali origjinal të reduktohet ose të bëhet më e thjeshtë.

Formula e zëvendësimit të ndryshueshme të ndryshueshme

Konsideroni shprehjen që qëndron nën shenjën integrale. Ai përbëhet nga një vepër e funksionit të integruar që ne tregojmë si f (x) dhe diferencial DX :. Le të shkojmë në variablin e ri duke zgjedhur disa raporti x \u003d x (t). Atëherë ne duhet të shprehim funksionin f (x) dhe DX diferenciale nëpërmjet variablit t.

Për të shprehur funksionin integrand f (x) Nëpërmjet një ndryshore t, ju vetëm duhet të zëvendësoni në vend të ndryshores X Raporti i zgjedhur X \u003d X (t).

Transformimi diferencial kryhet si vijon:
.
Kjo është, diferenca DX është e barabartë me produktin e X nga Derivative në diferencial DT.

Pastaj
.

Në praktikë, më shpesh rasti në të cilin kryejmë një zëvendësim, duke zgjedhur një ndryshore të re si një funksion nga Vjetër: t \u003d t (x). Nëse ne menduam se funksioni i integruar mund të përfaqësohet si
,
ku t ' (x) - Kjo është një derivat i t nga x, atëherë
.

Pra, formula bazë për zëvendësimin e ndryshores mund të përfaqësohet në dy lloje.
(1) ,
ku X është një funksion nga t.
(2) ,
ku t është një funksion nga x.

Shënim i rëndësishëm

Në tabelat integrale, ndryshorja e integrimit është më e shpeshtë e treguar si x. Megjithatë, vlen të merret parasysh se ndryshorja e integrimit mund të shënohet me çdo letër. Dhe për më tepër, si një ndryshore e integrimit mund të jetë ndonjë shprehje.

Si shembull, e konsideroni integrimin tabelor
.

Këtu X mund të zëvendësohet nga ndonjë ndryshore tjetër ose funksion nga variabli. Këtu janë shembuj të opsioneve të mundshme:
;
;
.

Në shembullin e fundit, duhet të kihet parasysh se kur kalon në një variabël të integrimit X, diferenca konvertohet si më poshtë:
.
Pastaj
.

Në këtë shembull, përfundoi thelbi i integrimit të zëvendësimit. Kjo është, ne duhet të mendojmë se
.
Pas kësaj, integrali zbret në tavolinë.
.

Ju mund ta llogarisni këtë integral duke zëvendësuar një ndryshore duke përdorur formulën (2) . Vënë t \u003d x 2 + X.. Pastaj
;
;

.

Shembuj të integrimit të zëvendësimit të ndryshueshëm

1) Llogarisni integruesin
.
Ne e vërejmë këtë (Sin x) '\u003d cos x. Pastaj

.
Këtu kemi aplikuar zëvendësimin t \u003d sin X..

2) Llogarisni integruesin
.
Ne e vërejmë këtë. Pastaj

.
Këtu kemi përfunduar integrimin e zëvendësimit të ndryshores t \u003d arctG X..

3) I integruar
.
Ne e vërejmë këtë. Pastaj

. Këtu, kur integrohet, një ndryshim i ndryshores t \u003d x 2 + 1 .

Zëvendësimet lineare

Ndoshta më të zakonshmet janë zëvendësimet lineare. Po zëvendëson një pamje të ndryshueshme
t \u003d AX + B,
ku A dhe B janë konstante. Me një zëvendësim të tillë, diferencat janë të lidhura me lidhjen
.

Shembuj të integrimit të zëvendësimeve lineare

A) Llogarisni integralin
.
Vendimi.
.

B) Gjej integrale
.
Vendimi.
Ne përdorim vetitë e funksionit indikativ.
.
ln 2. - Kjo është konstante. Llogarisni integralin.

.

C) Llogarisni integralin
.
Vendimi.
Ne japim një polinom katror në emëruesin e emërtimit në shumën e shesheve.
.
Llogarisni integralin.

.

D) Gjej integrale
.
Vendimi.
Ne konvertojmë një polinom nën rrënjë.

.
Ne integrojmë duke përdorur metodën e zëvendësimit të ndryshueshme.

.
Më parë kemi marrë një formulë
.
Nga këtu
.
Zëvendësimi i kësaj shprehjeje, marrim përgjigjen përfundimtare.

Por mënyrat për të sjellë integrals në tabelore Ne ju kemi listuar:

metoda e zëvendësimit të ndryshores;

metoda e intgning në pjesë;

Metodë e integrimit të drejtpërdrejtë

mënyrat e përfaqësimit të integraleve të pasigurta përmes tabelave për integrals nga fraksionet racionale;

metodat e përfaqësimit të integraleve të pasigurta përmes integraleve tabelare për integrals nga shprehjet iracionale;

metodat për shprehjen e integraleve të pasigurta përmes integraleve tabelare nga funksionet trigonometrike.

Funksioni i Përkohshëm Intecnite Integral

Ekpftuesi i pasigurt intelekt tregues

Por një logaritment i pacaktuar integral nuk është një integral tabelare, në vend të saj tabela është formula:

Integralet e pasigurta të funksioneve trigonometrike: Cosin dhe Integrals tangjent sinus

Integralet e pasigurta me funksione trigonometrike të kundërta

Tabletë ose metodë e integrimit të drejtpërdrejtë. Me ndihmën e konvertimeve identike të funksionit të integruar, integresa është zvogëluar në tërësi në të cilën zbatohen rregullat themelore të integrimit dhe është e mundur të përdoret tabela kryesore integrale.

Shembull

Detyrë. Gjej integrale

Vendimi. Ne përdorim vetitë e integralit dhe japim këtë pjesë integrale në tryezë.

Përgjigje.

Teknikisht metoda e zëvendësimit të ndryshores Në një integrim të pacaktuar zbatohet në dy mënyra:

– Duke përmbledhur funksionin nën shenjën e diferencialit. - Në të vërtetë duke zëvendësuar ndryshoren.

Duke përmbledhur funksionin nën shenjën e diferencialit

Shembulli 2.

Kryejnë kontroll.

Ne analizojmë funksionin integrand. Këtu kemi një pjesë, dhe në emërtimin një funksion linear (me "Xom" në shkallën e parë). Ne shikojmë në tryezën integrale dhe gjejmë më të ngjashme :.

Ne furnizojmë funksionin nën shenjën e diferencës:

Ata që janë të vështirë për të kuptuar menjëherë se sa duhet të shqetësoheni, mund të zbuloni shpejt diferencën në draftin :. Po, rezulton, kjo do të thotë se asgjë nuk ka ndryshuar, unë duhet të shumëzoj integralin. Tjetra, ne përdorim formulën e tryezës:

Kontrolloni: Funksioni fillestar integrand është marrë, që do të thotë se integrali gjendet në mënyrë korrekte.

Shembull 5.

Gjeni një integral të pacaktuar.

Si shembull, mora integralin, të cilin e konsideruam në fillim të mësimit. Siç kemi folur tashmë, për të zgjidhur integrale, një formulë tabelare Dhe unë do të doja të arrijnë atë.

Ideja e metodës së zëvendësimit është të shprehje komplekse (ose disa funksione) zëvendësoni me një letër. Në këtë rast, sugjeron: Letra e dytë më e popullarizuar për zëvendësim është letra. Në parim, letra të tjera mund të përdoren, por ne ende do t'i përmbahemi traditave.

Kështu që: Por kur zëvendësohet ne kemi! Ndoshta, shumë menduan se nëse kalon tranzicioni në një variabël të ri, atëherë në një integral të ri, gjithçka duhet të shprehet përmes letrës, dhe nuk ka vend ndryshe atje. Ndiqni një përfundim logjik që ju nevojitet të kthehet në një shprehje të caktuar që varet vetëm nga.

Veprimi tjetër. Pasi kemi marrë një zëvendësim, në këtë shembull, ne duhet të gjejmë diferencën. Me diferencat, unë mendoj se miqësia tashmë është themeluar.

Që atëherë,

Pas shkatërrimit të diferencialit, rezultati përfundimtar i rekomanduar për të rishkruar më së shpejti: Tani sipas rregullave të proporcionit, ne shprehim që ju nevojitet:

Përfundimisht: Në këtë mënyrë: Dhe kjo është tashmë më e madhe se as nuk ka një integral tabelare (Tabela, integrals, natyrisht, është e vlefshme për të dy ndryshoren).

Në përfundim, mbetet të zëvendësohet. Mos harroni se.

Gati.

Dizajni i fundosur i shembullit të konsideruar duhet të duket diçka e tillë:

“

Ne do të zëvendësojmë:

“

Ikona nuk mban ndonjë kuptim matematik, ai nënkupton që ne ndërpresim zgjidhjen për shpjegime të ndërmjetme.

Kur aplikoni për një shembull në një fletore, shënimi i kundërt është bërë më mirë me një laps të thjeshtë.

Vëmendje! Në shembujt e mëposhtëm, gjetja e diferencave nuk do të përshkruhet në detaje.

Dhe tani është koha për të kujtuar mënyrën e parë për të zgjidhur:

Qfare eshte dallimi? Nuk ka dallim themelor. Kjo është në të vërtetë e njëjta gjë. Por nga pikëpamja e dizajnimit të detyrës, metoda e përmbledhjes së funksionit nën shenjën e diferencës është shumë më e shkurtër. Lind pyetja. Nëse mënyra e parë është më e shkurtër, atëherë pse përdorni metodën e zëvendësimit? Fakti është se për një numër integralësh nuk është aq e lehtë për të "përshtatur" funksionin nën shenjën e diferencialit.

Integrimi në pjesë. Shembuj të zgjidhjeve

Integrals nga logarithm

Shembulli 1.

Gjeni një integral të pacaktuar.

Klasik. Herë pas here, ky integral mund të gjendet në tavolina, por është e padëshirueshme të përdorësh përgjigjen e gatshme, pasi mësuesi i avitaminozës së pranverës dhe është shumë e habitur. Sepse konsiderohet integrale nuk është një tabelë - ajo merret në pjesë. Ne vendosim:

Ne ndërpresim vendimin për shpjegime të ndërmjetme.

Përdorni formulën e integrimit në pjesë:

Formula aplikohet nga e majta në të djathtë

Ne shikojmë në anën e majtë :. Natyrisht, në shembullin tonë (dhe në të gjithë të tjerët që ne e konsiderojmë) diçka duhet të shënohet, dhe diçka për të.

Në integrals të llojit të konsideruar për të Gjithmonë nënkupton logaritalm.

Teknikisht, vendbanimi i zgjidhjes zbatohet si më poshtë, në kolonën shkruaj:

Kjo është, sepse ne kemi shënuar logaritm, dhe për - pjesa e mbetur Shprehje e integruar.

Faza tjetër: Gjeni diferencat:

Diferenciale është pothuajse e njëjtë me një derivativ, si ta gjesh atë, ne kemi çmontuar tashmë në mësimet e mëparshme.

Tani gjejmë një funksion. Për të gjetur tiparin duhet të integrohet pjesa e djathtë Barazia më e ulët:

Tani ne hapim zgjidhjen tonë dhe ndërtojmë anën e djathtë të formulës :. Nga rruga, dhe një mostër e një zgjidhjeje pistoni me shenja të vogla:

Momenti i vetëm, në punën që unë menjëherë riorganizova në vende dhe, pasi shumëzuesi pranohet të regjistrojë para logaritmit.

Siç mund ta shihni, përdorimi i formulës së integrimit në pjesë, në fakt, reduktoi zgjidhjen tonë për dy integrale të thjeshta.

Vini re se në disa raste menjëherë pas Përdorimi i formulës, nën integralin e mbetur, thjeshtimet janë të nevojshme - në shembullin në shqyrtim ne kemi ulur integrand në "X".

Kryejnë një kontroll. Për ta bërë këtë, ju duhet të merrni një të nxjerrë nga përgjigja:

Integrand fillestar është marrë, kjo do të thotë që integrali është zgjidhur si duhet.

Gjatë inspektimit, ne kemi përdorur sundimin e diferencimit të punës :. Dhe nuk është rastësisht.

Integrimi i formulës në pjesë dhe formulë - Këto janë dy rregulla të kundërta reciproke.

Integrals nga ekspozuesit shumëzuar me polinom

Rregulla e përgjithshme: mbrapa

Shembull 5.

Gjeni një integral të pacaktuar.

Duke përdorur një algoritëm të njohur, integruar në pjesë:

Nëse ka vështirësi me integrale, atëherë duhet të ktheheni në artikull Metodë për zëvendësimin e një ndryshoreje në një integrim të pacaktuar.

E vetmja gjë që mund të bëni është "krehja" përgjigja:

Por nëse informatika juaj e teknikës nuk është shumë e mirë, atëherë opsioni më i favorshëm për të lënë përgjigjen apo madje

Kjo është, një shembull është konsideruar i zgjidhur kur është marrë integrale e fundit. Nuk do të ketë gabim, një tjetër është se mësuesi mund të kërkojë të thjeshtojë përgjigjen.

Integralet nga funksionet trigonometrike të shumëzuara me polinom

Rregulla e përgjithshme: mbrapa Gjithmonë nënkupton polinom

Shembulli 7.

Gjeni një integral të pacaktuar.

Ne integrojmë në pjesë:

Hmmm, ... dhe nuk ka asgjë për të komentuar.