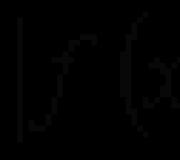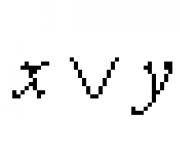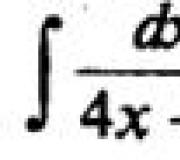§2 Kufiri i funksionit të dy variablave. Kufiri i funksionit të disa variablave kufizon funksionin e disa variablave në pafundësi

Konsideroni aeroplanin dhe sistemin Oksi koordinatat drejtkëndore Cartesian në të (mund të konsiderohen sisteme të tjera të koordinatave).

Nga gjeometria analitike ne e dimë se çdo palë e porositur e numrave (x, y) ju mund të krahasoni pikën e vetme M. aeroplan dhe anasjelltas, çdo pikë M. aeroplani korrespondon me një palë numrash të vetme.

Prandaj, në të ardhmen, duke folur për pikën, ne shpesh do të nënkuptojmë dy numrat përkatës (x, y) dhe anasjelltas.

Përkufizimi 1.2 Shumë palë numrash (x, y) Pabarazitë e kënaqshme quhet një drejtkëndësh (i hapur).

Në aeroplan është përshkruar nga një drejtkëndësh (Fig.12) me anët paralele me akset e koordinatave, dhe me qendrën në atë pikë M. 0 (X. 0 y. 0 ) .

Drejtkëndëshi pranohet të nënkuptojë simbolin e mëposhtëm:

Ne prezantojmë një koncept të rëndësishëm: lagjen e një pike.

Përkufizimi 1.3 drejtkëndëshe δ -Cost ( delta-lagje ) M. 0 (X. 0 y. 0 ) quajtur drejtkëndësh

me qendër në pikën M. 0 dhe me të njëjtën anë nga partitë 2δ. .

Përkufizimi 1.4 rrethore δ - Pika e lagjes M. 0 (X. 0 y. 0 ) quajtur gamën e rrezes δ me qendër në pikën M. 0 , i.e. shumë pikë M (xy) Koordinatat e të cilëve plotësojnë pabarazinë:

Është e mundur të futet konceptet e lagjeve dhe specieve të tjera, por për qëllime të analizës matematikore të detyrave teknike, përdoren vetëm një mjedis drejtkëndor dhe rrethor.

Ne prezantoj konceptin e ardhshëm të limitit të funksionit të dy variablave.

Le funksionin z \u003d f (x, y) të përcaktuar në një rajon ζ dhe M. 0 (X. 0 y. 0 ) - pika e shtrirë brenda ose në kufirin e kësaj zone.

Përkufizimi 1.5 Numri A. i quajtur funksioni limit f (x, y) për

nëse për ndonjë numër pozitiv ε ju mund të gjeni një numër të tillë pozitiv δ se pabarazi

kryhet për të gjitha pikat M (x, y) nga rajoni ζ përveç M. 0 (X. 0 y. 0 ) Koordinatat e të cilëve plotësojnë pabarazitë:

Kuptimi i këtij përkufizimi është se vlerat e funksionit f (x, y) ndërsa ju pëlqen pak ndryshojnë nga numri A në pikat e një lagjeje mjaft të vogël të pikës M. 0 .

Këtu, përkufizimi bazohet në një mjedis drejtkëndor. M. 0 . Do të ishte e mundur të konsideroni lagjen rrethore të pikës M. 0 dhe pastaj do të ishte e nevojshme të kërkohej përmbushja e pabarazisë

në të gjitha pikat M (x, y) rajon ζ përveç M. 0 dhe kushte të kënaqshme:

Distanca midis pikave M. dhe M. 0 .

Konsumohen përcaktimet e mëposhtme të kufirit:

Duke pasur parasysh kufirin në kufirin e funksionit të dy variablave, ju mund të transferoni teoremat kryesore për kufijtë për funksionet e një ndryshore në funksion të dy variablave.

Për shembull, kufiri i teoremave të shumës, punimeve dhe dy funksioneve private.

§3 Vazhdimësia e funksionit të dy variablave

Le funksionin z \u003d f (x, y) të përcaktuara në pikë M. 0 (X. 0 y. 0 ) dhe rrethinat e saj.

Përkufizimi 1.6 Funksioni quhet i vazhdueshëm në pikën M. 0 (X. 0 y. 0 ) , nese nje

Nëse funksioni f (x, y) vazhdueshme në pikën M. 0 (X. 0 y. 0 ) T.

Për aq sa

Kjo është, nëse funksioni f (x, y) vazhdueshme në pikën M. 0 (X. 0 y. 0 ) , increments pafundësisht të vogla të argumenteve në këtë fushë korrespondojnë me rritjen pafundësisht të vogël ΔZ. funksione z. .

Deklarata e kundërt: Nëse increments pafundësisht të vogla të argumenteve korrespondojnë me rritjen pafundësisht të vogël të funksionit, atëherë funksioni është i vazhdueshëm

Funksioni i vazhdueshëm në çdo pikë të rajonit quhet i vazhdueshëm në zonë. Për funksionet e vazhdueshme të dy variablave, si dhe për funksionin e një ndryshoreje, të vazhdueshme në segmentin, teoremat themelore Weierstrass dhe Bolzano - Cauchy.

Ndihmë: Carl Theodore Wilhelm Weierstrasse (1815 - 1897) - Matematikan gjerman. Bernard Bolzano (1781 - 1848) - Matematikan çeke dhe filozof. Augusten Louis Cauchy (1789 - 1857) - Matematikan francez, President i Akademisë Franceze të Shkencave (1844 - 1857).

Shembulli 1.4. Eksploroni funksionin e vazhdimësisë

Ky funksion përcaktohet me të gjitha vlerat e variablave. x. dhe y. Përveç fillimit të koordinatave, ku emëruesi shton zero.

Polinom x. 2 + y. 2 të vazhdueshme kudo, që do të thotë se rrënja katrore është e vazhdueshme nga funksioni i vazhdueshëm.

Pjesa do të jetë e vazhdueshme kudo, përveç pikave ku emëruesi është zero. Kjo është, funksioni në shqyrtim është i vazhdueshëm në të gjithë aeroplanin e koordinatave. Ohu , duke përjashtuar origjinën e koordinatave.

Shembulli 1.5. Eksploroni funksionin e vazhdimësisë z \u003d tg (x, y) . Tangente është përcaktuar dhe e vazhdueshme me të gjitha vlerat e fundme të argumentit, përveç vlerave të barabarta me një numër të rastësishëm të vlerave π / 2. . duke përjashtuar pikat ku

Me çdo fikse "K" ekuacioni (1.11) përcakton hiperbolën. Prandaj, funksioni në shqyrtim është një funksion i vazhdueshëm x dhe Y. , duke përjashtuar pikat që shtrihen në kthesa (1.11).

Konceptet e dy ose tre variablave që konsiderohen më lart mund të përgjithësohen në rast të variablave.

Përkufizimi.Funksion variabla
quajtur funksioni, definicion në terren
që i takon
, dhe gamën e vlerave është një aks i vlefshëm.

Një funksion të tillë të çdo grupi të variablave
i
mats numrin e vetëm .

Në të ardhmen, për siguri, ne do të shqyrtojmë funksionet
variablat, por të gjitha pretendimet e formuluara për funksione të tilla mbeten të vërteta për funksionet e një numri më të madh të variablave.

Përkufizimi. Numër quajtur kufirin e funksionit

në pikën
Nëse për secilin
ka një numër të tillë
se në të gjitha
nga lagja
Përveç kësaj pike, pabarazia kryhet

.

Nëse kufiri i funksionit
në pikën
korb Pastaj tregohet në formë

.

Pothuajse të gjitha vetitë e kufijve që konsiderohen më herët për funksionet e një ndryshore mbeten të vlefshme dhe për kufijtë e funksioneve të disa variablave, por ne nuk do të bëjmë praktikë gjetjen e kufijve të tillë.

Përkufizimi. Funksion
quajtur vazhdimisht në pikë
nëse kryhen tre kushte:

1) ekziston

2) Ekziston një funksion i funksionit në pikën

3) Këto dy numra janë të barabartë me njëri-tjetrin, i.e. .

Ju praktikisht mund të eksploroni vazhdimësinë e funksionit duke përdorur teoremen e mëposhtme.

Teorema. Çdo tipar elementar
të vazhdueshme në të gjitha pikat e brendshme (I.E. jo kufitare) të fushës së saj të përkufizimit.

Shembull. Gjeni të gjitha pikat në të cilat funksioni

të vazhdueshme.

Siç është përmendur më lart, kjo veçori është përcaktuar në një rreth të mbyllur.

.

Pikat e brendshme të këtij rrethi janë vazhdimësia e funksionit të dëshiruar të funksionit, i.e. funksion
të vazhdueshme në rrethin e hapur
.

Përcaktimi i konceptit të vazhdimësisë në pikat kufitare të fushës së përcaktimit
funksionet janë të mundshme, por ne nuk do ta shpenzojmë këtë pyetje në kurs.

1.3 increments private dhe derivatet private

Në kontrast me funksionet e një ndryshore, funksionet e disa variablave kanë lloje të ndryshme të increments. Kjo është për shkak të faktit që lëviz në aeroplan
nga pika
mund të kryhet në drejtime të ndryshme.

Përkufizimi. Rritje private për të funksione
në pikën
rritje korresponduese
dallimi quhet

Kjo rritje është në thelb duke rritur funksionin e një ndryshoreje
marrë nga funksioni
me një kuptim të vazhdueshëm
.

Të ngjashme me rritjen private për të Në pikën
funksione
rritje korresponduese
dallimi quhet

Kjo rritje llogaritet me një vlerë fikse.
.

Shembull. Lë

,
,
. Gjeni increments private të këtij funksioni dhe ne

Në këtë shembull, me vlera të barabarta të increments argument
dhe
, Increments private të funksionit doli të jenë të ndryshme. Kjo është për shkak të faktit se zona e drejtkëndëshit me palët
dhe
me anën në rritje në
rritet me përmasa
, dhe me anën në rritje në
rritet nga
(Shih Cris.4).

Nga fakti se funksioni i dy variablave ka dy lloje të increments, rrjedh se dy lloje të derivateve mund të përcaktohen për të.

Përkufizim. Privat rrjedh nga funksione
në pikën
e quajti kufirin e marrëdhënies së rritjes private ky funksion në pikën e specifikuar për të rritur
argument ato.

. (1)

Derivatet e tilla private tregohen nga simbolet ,,,. Në rastet e fundit, një letër e rrumbullakët " ” – “"Do të thotë fjala" private ".

Në mënyrë të ngjashme, një derivat privat në pikën
përcaktuar nga kufiri

. (2)

Përcaktime të tjera të këtij derivate private: ,,.

Derivatet e pjesshme janë të vendosura sipas rregullave të njohura për diferencimin e funksionit të një ndryshoreje, me të gjitha variablat, me përjashtim të kësaj funksioni dallojnë, konsiderohen konstante. Pra, kur qëndroni ndryshore është marrë për konstante, dhe kur - i përhershëm .

Shembull. Gjeni funksione private të nxjerra
.

,
.

Shembull. Ne gjejmë derivatet private të tre variablave

.

;
;
.

Funksionet e derivateve të pjesshme
karakterizojnë shpejtësinë e ndryshimit të këtij funksioni në rastin kur një nga variablat është fikse.

Shembull i ekonomisë.

Koncepti kryesor i teorisë së konsumit është funksioni i dobishëm
. Kjo veçori shpreh dobinë e shërbimeve
ku X është shuma e mallrave X, Y - numri i mallrave W. Pastaj derivatet private
do të quhet si shërbimet maksimale x dhe y. Shkalla maksimale e zëvendësimit
një produkt është i ndryshëm i barabartë me qëndrimin e përdorimit të tyre kufi:

. (8)

Detyra 1. Gjeni normën e kufirit të zëvendësimit H në funksionin e shërbimeve në pikën A (3.12).

Vendimi: Nga formula (8) marrim

Kuptimi ekonomik i normës së zëvendësimit të kufi është të mbështesë formulën
ku - Produkti i mallrave X, - Çmimi i mallrave u.

Përkufizimi. Nëse funksioni
ka derivatet private, diferencat e saj private quhen shprehje.

dhe

këtu
dhe
.

Diferencat private janë diferencat e funksioneve të një ndryshore të marrë nga funksioni i dy variablave.
me fiks ose .

Shembuj nga ekonomia. Konsideroni si një shembull funksionin e Kobba Douglas.

Vlerë - Produktiviteti mesatar i punës, pasi kjo sasi e produkteve (në terma vlerash) të prodhuara nga një punonjës.

Vlerë
- Midder fdo-vlerësim - sasia e produkteve në një makinë.

Vlerë
- Pajisjet e aksioneve të mesit - kostoja e fondeve, duke rënë për njësi të burimeve të punës.

Prandaj, një derivat privat
ajo quhet produktiviteti kufizues i punës, pasi është e barabartë me vlerën e shtuar të produkteve të prodhuara nga një punëtor tjetër shtesë.

Në mënyrë të ngjashme,
- Kufizoni FDO-Raportin.

Ekonomia shpesh është bërë pyetje: Sa për qind do të ndryshojë prodhimin e produkteve nëse numri i punëtorëve rritet me 1% ose nëse fondet rriten me 1%? Përgjigjet për këto pyetje japin konceptin e elasticitetit të funksionit me argument ose derivativ relativ. Ne do të gjejmë elasticitetin e prodhimit nga puna
. Duke zëvendësuar në numëruesin e llogaritur mbi derivat privat , marr
. Pra, parametri ka një kuptim të qartë ekonomik - kjo është elasticiteti i lirimit të punës.

E njëjta kuptim ka parametrin - Kjo është elasticiteti i fondeve në fonde.

Për të dhënë konceptin e kufirit të funksionit të disa variablave, kufizoni veten në rastin e dy variablave h. dhe w.. Nga funksioni i përkufizimit f (x, y)ka një kufi në pikën ( h. 0 , w. 0) të barabartë me numrin Porshënuar nga:

(shkruaj përsëri f (x, y)>Porpër (x, y)> (h. 0 , w. 0)) Nëse përcaktohet në një lagje të pikës ( h. 0 , w. 0), përveç, ndoshta, vetë pikë dhe nëse ka një kufi

Çfarëdo që viktima të ( h. 0 , w. 0) Sekuenca e pikëve ( x. k. , y. k.).

Gjithashtu, si në rastin e funksionit të një ndryshore, mund të futni një përcaktim ekuivalent të kufirit të funksionit të dy variablave: një funksion f. ka në pikën ( h. 0 , w. 0) Kufizoni të barabartë PorNëse përcaktohet në një lagje të pikës ( h. 0 , w. 0) me përjashtim të ndoshta pikës, dhe për ndonjë e\u003e 0 ka d\u003e 0 që

| f (x, y) - A. | < е (3)

per te gjithe (x, y)

0 < < д. (4)

Ky përkufizim, nga ana tjetër, është ekuivalente me sa vijon: për çdo e\u003e 0 ka një D-lagje të pikës ( h. 0 , w. 0) të tilla si për të gjithë ( x, Y.) nga kjo lagje përveç ( h. 0 , w. 0), Pabarazia (3) kryhet.

Që nga koordinatat e një pike arbitrare ( x, Y.) Pika lagje ( h. 0 , w. 0) Mund të shkruhet si x \u003d x. 0 + D. h., y \u003d u 0 + D. w., Barazia (1) është ekuivalente me barazinë e mëposhtme:

Konsideroni disa funksione të specifikuara në lagjen e një pike ( h. 0 , w. 0), përveç, ndoshta, vetë pikë.

Le sh \u003d (sh h. , Sh w.) - Njësia e Gjatësisë së Vektorit Arbitrar (| U | 2 \u003d h. 2 + sh w. 2 \u003d 1) dhe t. \u003e 0 - Scalar. Pikat e formularit ( h. 0 + t.sh h. , y. 0 + t.sh w.) (0 < t.)

formojnë një rreze që del nga ( h. 0 , w. 0) në drejtim të vektorit. Për të gjithë, ju mund ta konsideroni funksionin

f. (h. 0 + t.sh h. , y. 0 + t.sh w.) (0 < t. < д)

nga një ndryshore skalare t.ku D është një numër i vogël.

Kufiri i këtij funksioni (një ndryshore t.)

f. (h. 0 + t.sh h. , y. 0 + t.sh w.),

f. Në pikën ( h. 0 , w. 0) në drejtim.

Shembulli 1.Funksione

të përcaktuara në aeroplan ( x, Y.) Me përjashtim të pikës h. 0 = 0, w. 0 \u003d 0. Ne kemi (marr parasysh):

(Për e\u003e 0, ne supozojmë D \u003d e / 2 dhe pastaj | f (x, y)| < е, если < д).

nga e cila mund të shihet se kufiri i C në pikën (0, 0) në drejtime të ndryshme është krejt (rreze vektoriale e vetme y \u003d kx., h. \u003e 0, ka pamjen

Shembulli 2. Konsideroni B. R. 2 funksion

(h. 4 + w. 2 ? 0).

Kjo veçori në pikën (0, 0) për çdo të drejtpërdrejtë y \u003d kx.duke kaluar përmes origjinës së koordinatës, ka një kufi të barabartë me zero:

për h. > 0.

Megjithatë, ky funksion nuk ka një kufi në pikën (0, 0), për y \u003d x. 2

Ne do të shkruajmë nëse funksioni f. të përcaktuara në një lagje të pikës ( h. 0 , w. 0), përveç, ndoshta vetë pikë ( h. 0 , w. 0) dhe për të gjithë N. \u003e 0 Nuk është d\u003e 0 tillë që

| f (x, y)| > N.,

kohl së shpejti 0.< < д.

Ju gjithashtu mund të flisni për limitin f.kur h., w. > ?:

Porbarazia (5) duhet të kuptohet në kuptimin që për ndonjë e\u003e 0 ka të tilla N. \u003e 0 Çfarë për të gjithë h., w.Për kë x.| > N., |y.| > N.funksion f. të përcaktuara dhe ka pabarazi

| f (x, y) - Por| < е.

Barazi të barabartë

ku mund të jetë h. > ?, w. \u003e? Në të njëjtën kohë, si zakonisht, kufijtë (fundi) në pjesët e tyre të majtë ekzistojnë nëse ka kufizime f. dhe c.

Ne dëshmojmë për shembull (7).

Le ( x. k. , y. k.) > (h. 0 , w. 0) ((x. k. , y. k.) ? (h. 0 , w. 0)); pastaj

Kështu, kufiri në pjesën e majtë (9) ekziston dhe është i barabartë me pjesën e djathtë (9), dhe që nga sekuenca ( x. k. , y. k.) kërkon ( h. 0 , w. 0) Për çdo ligj, ky kufi është i barabartë me kufirin e funksionit f (x, y) C. (x, y) Në pikën ( h. 0 , w. 0).

Teorema. Nëse funksioni f (x, y) ka një kufi që nuk është i barabartë me zero në pikën ( h. 0 , w. 0), i.e.

pastaj ekziston d\u003e 0 tillë që për të gjithë h., w.Pabarazitë e kënaqshme

0 < < д, (10)

ajo kënaq pabarazinë

Prandaj, për ata (x, y)

ato. Ekziston një pabarazi (11). Nga pabarazia (12) për të specifikuar (x, y) Nga ku A\u003e 0 dhe në

A. < 0 (сохранение знака).

Nga funksioni i përkufizimit f (x) \u003d f (x 1 , …, x. n. ) \u003d A. ka një kufi në pikën

x. 0 \u003d e barabartë me numrin Porshënuar nga:

(shkruaj përsëri f (x) > A. (x. > x. 0)) Nëse përcaktohet në një lagje të pikës x. 0, përveç, ndoshta, është, dhe nëse ka një kufi

pavarësisht nga viktima x. 0 Sekuenca e pikëve h. k. nga lagja e specifikuar ( k. \u003d 1, 2, ...) përveç x. 0 .

Një tjetër përkufizim ekuivalent është si vijon: Funksioni f. Ka në pikë x. 0 kufizim i barabartë PorNëse përcaktohet në një lagje të pikës x. 0, me përjashtim të ndoshta, dhe për ndonjë e\u003e 0 ka d\u003e 0 që

per te gjithe h.Pabarazitë e kënaqshme

0 < |x - X. 0 | < д.

Ky përkufizim nga ana tjetër është ekuivalente me sa vijon: për çdo e\u003e 0 ka një lagje U (x. 0 ) pikë x. 0 tillë që për të gjithë xu (X. 0 ) , h. ? x. 0, Pabarazia (13) kryhet.

Natyrisht, nëse numri Por Ka një kufi f (x) në x. 0, T. Por Ka një funksion kufitar f (X. 0 + h) nga h. Në zero pikë:

dhe anasjelltas.

Konsideroni disa funksione f.të përcaktuara në të gjitha pikat e pikës së lagjes x. 0, me përjashtim të ndoshta pikave x. 0; Le sh \u003d (sh 1, ... p) - Njësia e gjatësisë së vektorit arbitrar (| uh | \u003d 1) dhe t. \u003e 0 - Scalar. Pikat e tipit x. 0 + t.sh (0.< t.) Forma me pamje x. 0 rreze në drejtim të vektorit. Për të gjithë, ju mund ta konsideroni funksionin

(0 < t. < д щ)

nga një ndryshore skalare t.ku kam një numër që varet. Kufiri i këtij funksioni (nga një ndryshore t.)

nëse ekziston, natyrisht telefononi limitin f. Në pikën x. 0 në drejtim të vektorëve.

Ne do të shkruajmë nëse funksioni f. të përcaktuara në disa mjedis x. 0, me përjashtim të ndoshta x. 0, dhe për të gjithë N. \u003e 0 Gjej d\u003e 0 tillë që f (x)| > N., që nga 0< |x - X. 0 | < д.

Ju mund të flisni për limitin f.kur h. > ?:

Për shembull, në rastin e një numri të caktuar Por Barazia (14) duhet të kuptohet në kuptimin që për ndonjë e\u003e 0 mund të specifikohet N. \u003e 0 që për pikat h.Për kë x.| > N.funksion f. Është e vendosur dhe pabarazia.

Pra, kufiri i funksionit f (x) = f (X. 1 , ..., h. p ) nga p Variablat përcaktohen me analogji në të njëjtën mënyrë si për një funksion të dy variablave.

Kështu, ne vazhdojmë të përcaktojmë kufirin e funksionit të disa variablave.

Numër Por quajtur kufirin e funksionit f (m) për M. > M. 0, nëse për ndonjë numër e\u003e 0 ka gjithmonë një numër të tillë d\u003e 0, i cili për çdo pikë M.përveç M. 0 dhe kushte të kënaqshme Mm. 0 | < д, будет иметь место неравенство | f (m) - Por | < е.

Kufiri është shënuar nga funksioni i dy variablave.

Teorema kanë të bëjnë me kufijtë. Nëse funksionon f. 1 (M) dhe f. 2 (M) për M. > M. 0 Kërkoni secilin deri në fund, pastaj:

Shembulli 1. Gjeni funksionin e limitit:

Vendimi. Ne e transformojmë kufirin si vijon:

Lë y \u003d kx., atëherë

Shembulli 2. Gjeni funksionin e limitit:

Vendimi. Ne përdorim kufirin e parë të mrekullueshëm atëherë

Shembulli 3. Gjeni funksionin e limitit:

Vendimi. Ne përdorim kufirin e dytë të mrekullueshëm atëherë

Departamenti: Matematika më e lartë

abstrakt

nën disiplinën "matematikë më e lartë"

Tema: "Kufiri dhe vazhdimësia e funksioneve të disa variablave"

Tolyatti, 2008.

Prezantimi

Koncepti i funksionit të një ndryshori nuk mbulon të gjitha varësitë që ekzistojnë në natyrë. Edhe në detyrat më të thjeshta, vlerat e të cilave përcaktohen nga grupi i vlerave të shumta të disa sasive.

Për të studiuar këto varësi, koncepti i një funksioni të disa variablave është futur.

Koncepti i një funksioni të disa variablave

Përkufizimi. Vlerë u. quajtur funksioni i disa variablave të pavarur ( x., y., z., …, t.) Nëse çdo grup vlerash të këtyre variablave vihet në përputhje me një vlerë të caktuar të madhësisë u..

Nëse variabli është një funksion nga dy variabla h.dhe w., atëherë varësia funksionale është shënuar

z. = f. (x., y.).

Simbol f. Përcakton këtu një sërë veprimesh ose rregull për të llogaritur vlerën z. Sipas kësaj pjese të vlerave h.dhe w..

Pra, për funksion z. = x. 2 + 3xy.

për h. \u003d 1 I. w. \u003d 1 kanë z. = 4,

për h. \u003d 2 I. w. \u003d 3 kanë z. = 22,

për h. \u003d 4 I. w. \u003d 0 kanë z. \u003d 16, etj.

I quajtur në mënyrë të ngjashme vlerën u.funksion nga tre variabla x., y., z., nëse rregulli është dhënë si në këtë vlera të trefishtë x., y. dhe z. Llogaritni vlerën e duhur u.:

u. = F. (x., y., z.).

Këtu simbol F. Përcakton grupin e veprimeve ose rregullit për të llogaritur vlerën u.Në përputhje me këto vlera x., y. dhe z..

Pra, për funksion u. = xy. + 2xz. – 3yz.

për H. = 1, w. \u003d 1 I. z. \u003d 1 kanë u. = 0,

për H. = 1, w. \u003d -2 I. z. \u003d 3 kanë u. = 22,

për H. = 2, w. \u003d -1 I. z. \u003d -2 kanë u. = -16, etj.

Kështu, nëse për shkak të ndonjë ligji të çdo tërësie p numra ( x., y., z., …, t.) nga disa grupe E.vënë në përputhje me një vlerë të caktuar të ndryshores u., se unë. u. quajtur funksion ot p variabla x., y., z., …, t.të përcaktuara në grup E.dhe është caktuar

u. = f.(x., y., z., …, t.).

Variabla x., y., z., …, t. I quajtur argumentet e funksionit, të vendosur E. - Zona e definicionit të funksionit.

Vlera private e funksionit është vlera e funksionit në një moment M. 0 (x. 0 , y. 0 , z. 0 , …, t. 0) dhe shënohet f. (M. 0) = f. (x. 0 , y. 0 , z. 0 , …, t. 0).

Zona e definimit të funksionit është grupi i të gjitha vlerave të argumenteve që korrespondojnë me çdo vlerësim të vlefshëm të funksionit.

Funksioni i dy variablave z. = f. (x., y.) hapësira duket të jetë një sipërfaqe. Që është, kur pika me koordinatat h., w. Drejtimin e të gjithë zonës së definicionit në terren të vendosur në aeroplan houNë përputhje me pikën hapësinore, në përgjithësi, përshkruan sipërfaqen.

Funksioni i tre variablave u. = F. (x., y., z.) Konsideroni si një funksion të pikës së një grupi të caktuar të pikave tre-dimensionale. Në mënyrë të ngjashme, një funksion p variabla u. = f.(x., y., z., …, t.) E konsiderojnë si funksion të një pike të disa p- hapësirë \u200b\u200bdimensionale.

Kufizimi i funksionit të disa variablave

Për të dhënë konceptin e kufirit të funksionit të disa variablave, kufizoni veten në rastin e dy variablave h. dhe w.. Nga funksioni i përkufizimit f. (x., y.) ka një kufi në pikën ( h. 0 , w. 0) të barabartë me numrin Porshënuar nga:

(shkruaj përsëri f. (x., y.) →Porpër (x., y.) → (h. 0 , w. 0)) Nëse përcaktohet në një lagje të pikës ( h. 0 , w. 0), përveç, ndoshta, vetë pikë dhe nëse ka një kufi

Çfarëdo që viktima të ( h. 0 , w. 0) Sekuenca e pikëve ( x K., y k.).

Gjithashtu, si në rastin e funksionit të një ndryshore, mund të futni një përcaktim ekuivalent të kufirit të funksionit të dy variablave: një funksion f. ka në pikën ( h. 0 , w. 0) Kufizoni të barabartë PorNëse përcaktohet në një lagje të pikës ( h. 0 , w. 0) me përjashtim, ndoshta vetë pikë, dhe për çdo ε\u003e 0 ka δ\u003e 0 që

| f. (x., y.) – A.| < ε(3)

per te gjithe (x., y.) Pabarazitë e kënaqshme

Ky përkufizim, nga ana tjetër, është ekuivalente me sa vijon: për çdo ε\u003e 0 ka një δ-lagje të pikës ( h. 0 , w. 0) të tilla si për të gjithë ( x., y.) nga kjo lagje përveç ( h. 0 , w. 0), Pabarazia (3) kryhet.

Që nga koordinatat e një pike arbitrare ( x., y.) Pika lagje ( h. 0 , w. 0) Mund të shkruhet si x \u003d x. 0 + Δ h., y \u003d u 0 + Δ w., Barazia (1) është ekuivalente me barazinë e mëposhtme:

Konsideroni disa funksione të specifikuara në lagjen e një pike ( h. 0 , w. 0), përveç, ndoshta, vetë pikë.

Le ω \u003d (ω H., ω W.) - Njësia e Gjatësisë së Vektorit Arbitrar (| ω | 2 \u003d ω H. 2 + ω. W. 2 \u003d 1) dhe t. \u003e 0 - Scalar. Pikat e tipit

(h. 0 + t.ω H., y. 0 + t.ω W.) (0 < t.)

formojnë një rreze që del nga ( h. 0 , w. 0) në drejtim të vektorit ω. Për çdo ω, ju mund ta konsideroni funksionin

f.(h. 0 + t.ω H., y. 0 + t.ω W.) (0 < t.< δ)

nga një ndryshore skalare t.ku δ është një numër i vogël.

Kufiri i këtij funksioni (një ndryshore t.)

nëse ekziston, natyrisht telefononi limitin f. Në pikën ( h. 0 , w. 0) në drejtim të ω.

Shembulli 1.Funksione

të përcaktuara në aeroplan ( x., y.) Me përjashtim të pikës h. 0 = 0, w. 0 \u003d 0. Ne kemi (marr parasysh atë

(Për ε\u003e 0, ne supozojmë δ \u003d ε / 2 dhe pastaj | f. (x., y.) | < ε, если

nga e cila mund të shihet se kufiri φ në pikën (0, 0) nga drejtime të ndryshme është përgjithësisht i ndryshëm (një rreze vektoriale e vetme y. = kx., h. \u003e 0, ka pamjen

Shembulli 2. Konsideroni B. R. 2 funksion

Kjo veçori në pikën (0, 0) për çdo të drejtpërdrejtë y. = kx.duke kaluar përmes origjinës së koordinatës, ka një kufi të barabartë me zero:

Megjithatë, ky funksion nuk ka një kufi në pikën (0, 0), për y \u003d x. 2

Do të shkruaj

|f. (x., y.) | > N.,

kohl së shpejti 0.<

Ju gjithashtu mund të flisni për limitin f.kur h., w. → ∞:

Për shembull, në rastin e një numri të caktuar Porbarazia (5) duhet të kuptohet në kuptimin që për çdo ε\u003e 0 ka të tilla N.\u003e 0 Çfarë për të gjithë h., w.Për kë x.| > N., |y.| > N.funksion f. të përcaktuara dhe ka pabarazi

Kufiri i funksionit të dy variablave.
Koncept dhe shembuj të zgjidhjeve

Mirë se vini në mësimin e tretë në temë FnpKur të gjitha shqetësimet tuaja më në fund filluan të realizohen \u003d) sa më shumë të dyshuar, koncepti i limitit zbatohet për funksionin e një numri arbitrar të argumenteve, të cilat ne duhet të merremi sot. Megjithatë, ekziston një lajm optimist. Është se me kufirin në një farë mase, abstrakti dhe detyrat përkatëse janë jashtëzakonisht të rralla në praktikë. Në këtë drejtim, vëmendja jonë do të fokusohet në kufijtë e funksionit të dy variablave ose, siç e shkruajmë më shpesh :.

Shumë ide, parime dhe metoda janë të ngjashme me teorinë dhe praktikën e kufijve "të zakonshëm", dhe për këtë arsye, në momentin që duhet të jetë në gjendje për të gjetur kufijtë Dhe më e rëndësishmja kuptojnë se çfarë është kufiri i funksionit të një ndryshoreje. Dhe, meqë fati së shpejti ju udhëhoqi në këtë faqe, atëherë, ka shumë të ngjarë, tashmë e dini se sa njerëz e dinë. Dhe nëse nuk ka - asgjë të tmerrshme, të gjitha boshllëqet me të vërtetë mbushin një çështje të orëve dhe madje minuta.

Ngjarjet e këtij profesioni po shpalosen në botën tonë tridimensionale, prandaj thjesht do të jenë një lëshim i madh për të mos marrë në to një pjesëmarrje të gjallë. Së pari, të paditurit është i njohur mirë sistemi Koordinues Cartesian në hapësirë. Le të ngrihemi dhe të shkojmë pak rreth dhomës ... ... kati për të cilin shkoni - ky është një avion. Ne kemi vënë kudo diku ... mirë, për shembull, në çdo qoshe, në mënyrë që të mos shqetësohen në rrugë. Të shkëlqyera. Tani, ju lutem shikoni dhe imagjinoni se batanije pikturuar flashed atje. ai sipërfaqetë përcaktuara nga funksioni. Lëvizja jonë në dysheme, pasi është e lehtë për t'u kuptuar, imiton ndryshimin në variablat e pavarur, dhe ne mund të lëvizim ekskluzivisht nën batanije, i.E. në fushat e përcaktimit të funksionit të dy variablave. Por më interesante fillon. E drejta mbi majën e hundës në batanije zvarritet një tarakacker të vogël, ku jeni atje dhe ai. Le ta quajmë atë Freddie. Lëvizja e saj simulon një ndryshim në vlerat e funksionimit përkatës. (përveç rasteve kur sipërfaqja ose fragmentet e saj janë paralele me aeroplanin dhe lartësia nuk ndryshon). I dashur lexues me emrin Freddie, mos u ofendoni, kështu që është e nevojshme për shkencën.

Merrni në duart tuaja të qepura dhe të përzënë batanije në një pikë arbitrare, lartësia e të cilit është shënuar, pas së cilës një mjet në dysheme është në mënyrë rigoroze nën vrimë, do të jetë një pikë. Tani duke filluar pafundësisht të ngushtë qasje , dhe qasja që kemi të drejtën e çdo trajektore (Çdo pikë e të cilave, natyrisht, është përfshirë në zonën e definicionit). Nëse në të gjitha rastet Freddie do pafundësisht të ngushtë Dërgoni në një birë në lartësi dhe pikërisht kjo lartësi, funksioni ka një kufi në pikën kur :

Nëse, sipas kushteve të specifikuara, pika e shënimit është e vendosur në buzë të batanije, kufiri do të ekzistojë ende - është e rëndësishme që lagje e bollshmeslate është të paktën disa pika nga funksioni i përcaktimit të funksionit. Përveç kësaj, si në rastin e funksioni limit i një ndryshore, i parëndësishëmnëse funksioni është përcaktuar në pikën apo jo. Kjo është, shpimi ynë mund të ftohet me një faqe (mendoni se funksioni i dy variablave është i vazhdueshëm) Dhe kjo nuk do të ndikojë në situatën - mos harroni se thelbi i kufirit nënkupton përafrimi pafundësisht i ngushtë, jo "qasje të saktë" deri në pikën.

Megjithatë, jeta pa re është lënë në hije nga fakti se, ndryshe nga vëllai i tij më i ri, kufiri nuk ekziston shumë më shpesh. Kjo është për shkak të faktit se ka shumë rrugë në një pikë ose në një tjetër në aeroplan, dhe secili prej tyre duhet të udhëheqë Freddie në mënyrë rigoroze për shpimet (opsionale "COWING-Up") Dhe në mënyrë rigoroze në lartësi. Dhe sipërfaqet e çuditshme me njëlloj të çuditshëm thyen të paktën të dua, gjë që çon në një shkelje të kësaj gjendjeje të vështirë në disa pika.

Ne organizojmë shembullin më të thjeshtë - të marrë thikë në duart dhe të prerë batanije në mënyrë që pika e shënimit të shtrihej në vijën e prerë. Vini re se kufiri Ende ekziston, e vetmja gjë që kemi humbur të drejtën për të hyrë në pikën nën vijën e prerjes, pasi që kjo faqe "ra" nga zonat e definicionit të funksionit. Tani në mënyrë të rregullt ngre pjesën e majtë të batanije përgjatë boshtit, dhe pjesa e duhur e saj, përkundrazi, rrëshqisni ose madje e lini atë në vend. Çfarë ndryshoi? Dhe ndryshoi rrënjësisht sa më poshtë: Nëse tani do të afrohemi në pikën në të majtë, atëherë Freddie do të jetë në lartësi më të madhe se nëse iu afruam kësaj pike në të djathtë. Kështu, kufiri nuk ekziston.

Sigurisht, kufij të mrekullueshëmku pa to. Konsideroni instruktive në të gjitha shqisat një shembull:

Shembulli 11.

Ne përdorim për të dhimbur një formulë trigonometrike të njohur, ku dhe pranimin standard artificial duke organizuar kufijtë e parë të mrekullueshëm :

Le të kthehemi në koordinatat polare:
Nese atehere

Duket se vendimi shkon në një kryqëzim natyror dhe asgjë nuk parasheh probleme, por në fund të fundit ekziston një rrezik i madh për të lejuar një keqpërdorim të rëndë, për karakterin e të cilit unë kisha lënë të kuptohet tashmë në shembullin 3 dhe përshkruar në detaje pas shembullit 6. Së pari, përfundimi, atëherë koment:

Le të kuptojmë se pse do të jetë e keqe vetëm "pafundësi" ose "plus pafundësi". Le të shohim emëruesin: Që, që, rreze polare është e angazhuar për të pafundësisht të vogla Vlera pozitive :. Për më tepër ,. Kështu, shenja e emërtimit dhe të gjithë kufirin varet vetëm nga kosinu:
Nëse këndi polar (Koordinatat e 2 dhe 3-të të koordinatave :);
Nëse këndi polar (Koordinat e 1 dhe 4 të katërt :).

Gjeometrik, kjo do të thotë që nëse i afroheni fillimit të koordinatave në të majtë, atëherë sipërfaqja e përcaktuar nga funksioni , shtrihet në pafundësi poshtë: